The HMM is a latent variable model where the observed sequence of variables ![]() are assumed to be generated from a set of temporally connected latent variables
are assumed to be generated from a set of temporally connected latent variables ![]() .
.
The joint distribution of the observed variables or data ![]() and the latent variables
and the latent variables ![]() can be written as :
can be written as :
![Rendered by QuickLaTeX.com \[p(x, y)=p(x|y)p(y)\,=\,\prod_{t=1}^{T}p(x_{t}|y_{t})p(y_{t}|y_{t-1})\]](https://machinelearninginterview.com/wp-content/ql-cache/quicklatex.com-da9e1e96bca390bd552f19abd2ecce7a_l3.png)
One possible interpretation of the latent variables in the HMM model is that they are POS tags. We will go with this interpretation for simplicity, though the latent states could mean other things as well.
To generate text from a HMM, we need to know the transition matrix (the probability of going from one tag to another) and the emission/output matrix (the probability of generating a token given the tag.) Given this :
- First generate the state (tag)
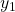 .
. - We then generate all the other tags using
![Rendered by QuickLaTeX.com \[p(y_{t}|y_{t-1})\]](https://machinelearninginterview.com/wp-content/ql-cache/quicklatex.com-43cd1bd51c02450c0b4808174f4b5079_l3.png)
.
- Then from each tag, generate a word(at each position
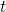 ) using the distribution
) using the distribution
![Rendered by QuickLaTeX.com \[p(x_{t}|y_{t})\]](https://machinelearninginterview.com/wp-content/ql-cache/quicklatex.com-7682bae29d2e4c1309826c512656ee55_l3.png)
.
Note that this is possible because given the current tag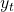 , observed variable
, observed variable 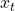 doesn’t depend on
doesn’t depend on 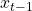 and
and 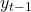 .
.
